BEAUTIFUL UNIVERSE:

TOWARDS RECONSTRUCTING PHYSICS
FROM NEW FIRST PRINCIPLES

By Vladimir F. Tamari

4-2-8-C26 Komazawa, Setagaya-ku, Tokyo Japan 154-0012

vladimirtamari@hotmail.com

(First published on this website and circulated by email from 10 July 2005. Material related to the Compton Effect and Dark Energy in sections 2.6 and 2.11 was added in November 2010)

ABSTRACT

Key words: Physical Theory. Theory of everything. TOE . Special Relativity, General Relativity. Node. Lattice. Quantum Mechanics. Uncertainty relations. Discrete Calculus. Ether, Heaviside. Planck’s Constant. EPR. Expanding Universe. Inflation. Anomaly.

1.      THE BEAUTIFUL UNIVERSE (BU) MODEL

1.1       THE NEED FOR REALISTIC THEORIES CLOSE TO NATURE

             Nature is now complex, but is believed to have evolved systematically over billions of years, following simple processes. This is the lesson of the theories of evolution[1], of fractal equations[2], cross-stitch embroidery[3], digital philosophy[4], and of Wolfram’s book A New Kind of Science[5]: A very simple effect, principle, rule or algorithm applied repeatedly leads to a very rich and complicated outcome.  In their efforts to discover the laws of nature, however, philosophers and physicists in different eras and belonging to different cultures were guided not only by their own thoughts and chance discoveries, but also by the intellectual baggage of their time: the accumulated knowledge , preconceived ideas, and even theological concepts.

            It is no wonder then that present-day physics is a hodge-podge of complicated ideas that do not always work well together, if at all. For example the theory describing gravity on a large scale, General Relativity (GR)[6] and the theory describing atomic and nuclear processes, Quantum Mechanics (QM)[7], speak different ‘languages’ describing what in the end must be the same phenomena. Moreover both (GR) and (QM), although extremely successful in predicting experimental results, both use non-intuitive ideas that seem far from reality. As with the preceding classical physics of Galileo and Newton, these theories describe the behavior of space, mass, time, or gravitation, but give no inkling of what these entities are. A lack of a self-consistent physical model of nature at its most basic level has allowed physicists to accept almost without question some of the more bizarre conclusions of (QM) such as instantaneous interaction at cosmic distances.  This contradicts a basic premise of Special Relativity (SR)[8] that signals cannot travel faster than the speed of light.

           Such confusion is possible because vastly different mathematical models to describe the same physical phenomena can be derived: even within (QM) itself, Schrödinger’s wave equation[9] was found to be exactly equivalent to a very different mathematical model, Heisenberg’s matrices[10].  But if a model is not ‘true to nature’ its very success distracts from other possibilities, blocking further progress. That happened with Ptolemy’s concept of the Earth staying still while the Sun and the planets rotated around it in complicated circular epicycles[11]. The system ‘worked’ even succeeding in predicting eclipses, because relative to an observer on Earth that is how the planets seemed to move. However it was not until Copernicus[12] put the Sun at the center that Kepler[13] could discover the much simpler elliptical orbits for the planets, paving the way for Newton’s law of gravitation[14] and modern physics.

            Similarly, although the concept of flexible spacetime ‘works’ in (SR)  and (GR), and that of probability waves ‘works’ in (QM), they are just mathematical ideas that must be discarded if better models closer to nature can be found. This is more than just a way to seek more elegant theories:  understanding nature at its own level is a necessary step to pave the way for further theoretical, experimental and technological discoveries. The human brain evolved over millions of years in organisms that interacted directly, causally and locally with inanimate nature on a molecular scale[15]. Is it too much to ask now that our understanding of Mother Nature should also be as simple, direct and realistic as possible?

1.2       A NEW START

           There is a widely recognized need to ‘start all over’[16], using the hard-won results of 20^th Century physics, but reconstructing them out of a few basic self-consistent premises.

            In the last few decades a great number of papers and books introduced new starting points at various levels of sophistication and completeness: Twistor Theory[17], various theories based on an ether particle[18], Quantum Gravity[19] and many others. String Theory[21] represents such a new start but it creates even more complications with ten or more dimensions using new mathematics, making the theory unlikely to be true to nature in the sense discussed above.

           The ideas behind Beautiful Universe (BU), the model presented here, derived from my discovery that a classical dipole’s electromagnetic potential field and its streamlines form a miniature united field from which can be derived many of the known phenomena of (SR), (GR), and (QM)[22].  (BU) theory describes a whole universe made up of charged particles spinning as dipoles, (including regions of dark matter where the particles have no spin). In the following sections, the (BU) model will be presented from first principles. In Section 2 an attempt will be made to show that the experimental results, but not the assumptions or all the methods of Newtonian physics, (SR), (GR) and (QM) and related cosmological theories may eventually be derived simply and directly from (BU).  In Section 3 experiments that may prove the correctness of the (BU) approach are proposed. The (BU) presented here is incomplete, and the treatment is qualitative and elementary. The aim is to gain a sure physical understanding of the proposed model’s basic concepts, leaving to future work the necessary but more abstract task of describing it systematically, quantitatively and mathematically.

1.3       A NETWORK OF CHARGED NODES CREATES SPACE AND TIME

            It is hypothesized that the entire universe is made up of an ordered lattice of identical spherically-symmetric charged nodes that are smaller than the smallest known nuclear particle, but are on a similar scale to it.  This network of nodes creates space itself, so it is meaningless to speak of the shape of an individual node, neither of the material it is made of, or its behavior nor of any space between nodes. Nevertheless to facilitate our understanding, a node can be thought of as being spherical, capable of spinning freely in place around any axis passing through its center. Either at cosmological initial conditions or during the universe’s later development, volumes of nodes rotate and interact with other volumes rotating in an opposite direction (FIG. 1).

           This cosmic angular momentum is acquired by individual nodes, and can be transmitted to neighboring nodes without friction, but will never disappear, conserving angular momentum locally and in the universe as a whole. Again, we can use the terms of classical physics here only as an analogy, but having like charge, the nodes repulse each other and create an expanding universal space.  It is theorized that individual nodes all over the universe spin in the same direction around their own axis.

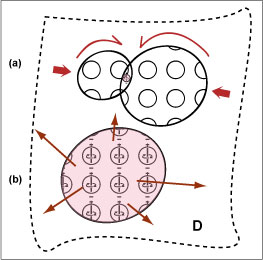FIG. 1. An imagined scenario for the creation of spin in nodes. (a) Two volumes of charged particles impinge on each other, as each volume rotates in the opposite directions. Their interaction causes individual nodes to acquire spin.(b) The resulting volume of spinning magnetized nodes self-assemble to creates an expanding space. There is also the possibility that the nodes exist within other undetected dimensions D (dashed outline).

  Spin plays a central role in (BU) and both the physical situation and the terms used should be clear.  There is first the ‘rotation’ of vast volumes of nodes without the individual nodes spinning on their axis (FIG. 1).  A dark-matter node is one without spin (FIG. 2a).

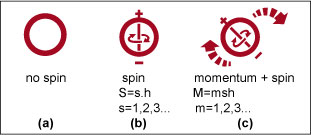FIG. 2 the three possible states of nodes (a) basic charged node. (b) Spinning around one axis, with angular momentum in units of Planck’s constant h. (c) Spinning around two axes creates forward momentum (large arrows).

           ‘Spin’ is when an individual node rotates around its axis so that it becomes a magnetic dipole (FIG. 2 b) with angular momentum in units of (h) without affecting adjacent nodes.  ‘Forward momentum’ is when the magnetic dipole spins on another axis orthogonal to the dipole axis.  The word ‘forward’ is used because such spin causes adjacent nodes to rotate, as follows:

           When spinning, a node becomes a magnetic dipole and generates Coulomb-like interactions[23] between neighboring dipoles. In a static field of adjacent spinning nodes the (+ +) and (- -) poles repulse each other until an all the nodes are so oriented that a state of equilibrium is reached, even though each node continues to spin around its own fixed axis.  When a node acquires forward spin, additional angular momentum in multiples of Planck’s constant[24] (h = 6.626068 × 10^-34 m² kg / s) is generated, (FIG. 2c) and this momentum (p) is passed on completely without ‘friction’ and distributed to the immediately adjacent nodes in the forward direction. When this occurs the magnetic dipole axis of the recipient node will twist according to the amount of momentum it received.

           When two or more spinning nodes in a field are forced to lock in place with opposite poles attracting, (+ -) or (- +) static structures of matter are created (FIG. 3).

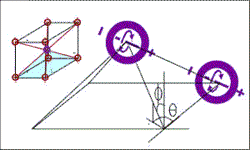FIG. 3 A simple particle forms when two spinning nodes change their orientation and are ‘locked’ because of the attraction of (+ -) poles.  The orientation angles of the node axes,, and their polyhedral arrangements define the possible ‘quantum spin’ states of the particle.

           This in turn sets the spin orientation and energy of all other surrounding nodes.  It is suggested that the term ‘quantum spin’ be used when referring to spin as it is now used in (QM). ‘Quantum spin’ does not define a rotation around an axis, but the possible symmetries of a particle in space.

           Everything in (BU), space, energy, radiation, matter is just patterns of nodes rotating in place and forming the universal lattice.  Apart from this rotation around various axes sharing fixed centers,  it is assumed that a node never rolls freely in space, bounces against matter, collides with other nodes like billiard balls, or flows like a grain in shifting sand A vast volume of nodes might conceivably slide, shearing from an adjacent volume, leaving an inhomogeneous ‘fracture’ in the lattice. This will not be considered here, where it will be assumed that node centers are always fixed, and only angular momentum is transferred from one node to its neighbor. 

            The (BU) interactions described above may be all the necessary and sufficient premises needed to describe all of the known phenomena of physics at its most basic level.

1.4        RADIATION IN VACUUM

          Coulomb-like repulsion and attraction between the spinning magnetized nodes and self-assembly create a minimum-energy arrangement of nodes in equilibrium that we know as the vacuum.  All the nodes forming the vacuum have identical spin

(1)                    s_o=h       

           The square-face Kepler packing was recently proven to be the densest packing possible for spheres[25] (FIG. 4), and Gauss proved that the face-centered cubic (FCC) packing is the densest lattice possible[26].  The (FCC) occurs in nature, for example ZnS, or zinc blende, has a face-centered cubic arrangement of sulfide ions with zinc ions in every other tetrahedral hole. An FCC and its tetrahedral components are shown in (FIG. 4).

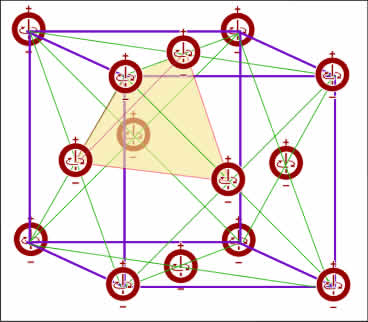FIG. 4 Self-assembly of magnetic dipole nodes oriented in the same direction as a Kepler packing. Each unit of the packing forms a cube with a node at each corner, with another node where the cube’s diagonals cross. The smallest regular volume made up of four nodes would be a tetrahedron (shaded).

           To maintain this state of minimum energy, the axes of the nodes in vacuum are in static equilibrium and as nearly parallel as possible. On the other hand, there exists the possibility that besides their usual rotation about their spin axis, the axis itself is also rotating about its center, so that all nodes in the universe are in synchronous rotation around two axes at once unless disturbed. Such rotation in unison would prevent the + and – poles of adjacent nodes in vacuum from clumping up because of the attractive Coulomb forces.

           The cubic symmetries of the node packing are responsible for the three dimensions of space. It is unnecessary here to speculate whether the nodes are set in yet one or more other hidden dimensions, causing their assumed behavior. This possibility, however, would raise the question of the universe having a center, with unequal distance and time scales in radial or tangential directions as shown in Fig. 36  below.

           Electromagnetic waves are created when an arrangement of matter loses equilibrium and forward angular momentum is released successively from node to neighboring node in a falling-domino effect.  A given node now possesses spin s_v in integral multiples of (h).

(2)                    s_v= j s_o =jh        (j=1,2,3…)­

creating a magnetic effect and capable of forward momentum. In a process similar to magnetic induction, each node transfers all of its momentum to the handful of nodes in ‘front’ of it in the lattice dividing its energy between them as in (FIG. 5).

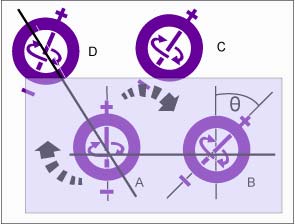FIG. 5 Forward momentum (large arrows) is transferred from node A to neighboring nodes. B gains most of the momentum, since it shares the plane (shaded) in which contains both of their spin axes. This gain in angular momentum causes B to twist by an angle . Lesser twisting is experienced by node D whose axis is normal to that of the forward momentum of A. Other nodes such as C in diagonal directions from A, twist at even lesser angles.

           This transfer is complete and lossless, and when two or more pulses arrive at a given node simultaneously, they superpose and interfere, adding their momentum linearly as vectors (FIG. 6).

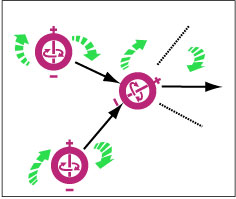
FIG. 6. Two modes contributing their momentums to the adjoining node to the right. The momentums add vectorially and interfere according to their phases.

           All the momentum of the donor node is passed to the adjacent nodes and propagates forward and outwards, spreading from node to node within the lattice (FIG. 7).  How much momentum each node receives and in what direction requires careful analysis: a node directly aligned with the momentum vector will get more forward momentum than that located diagonally to the side.  As a result of these interactions the nodes in free space acquire different amounts of spin and align themselves in various orientations. The resulting fields will have equipotential surfaces _constant where  the change of angle between neighboring nodes is constant.  Normal to _constant , the field streamlines are the paths along which the energy of the field is initially propagated. If the field is in equilibrium the nodes settle in unchanging orientation, and  indicate the field curvature. If momentum is continually being transferred a radiation field is the result as in (FIG. 7).

           As each charged node spins it creates its own magnetic B and electric E fields within itself. These effects only appear when the spinning behavior of adjoining nodes is affected.  The use of the B and E terms here is assumed ad hoc, and is only justified by what we know of the macroscopic behavior of radiation, and not from basic principles. On the scale of the nodes, it is not possible to speak of a continuous streamline line joining three or more congruent nodes, because of the step-like geometry of the packing.  However, along a line of successive nodes the spin axis changes direction in a harmonic motion similar to that of (FIG. 8)

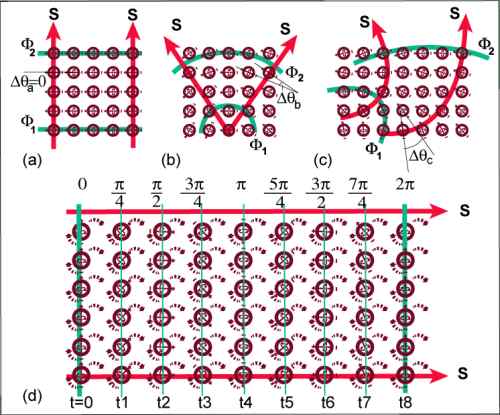
FIG. 7.  Fields in (BU) can be in equilibrium (a), (b), (c), or time varying radiation fields (d). In all cases equipotential surfaces () are where node-to-node orientation  is constant. Streamlines (S) are normal to (). (d) The nodes in a radiation field transfer angular momentum along (S) so that nodes on successive (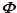) have different phase angles  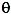at various times t0,t1,t2,…

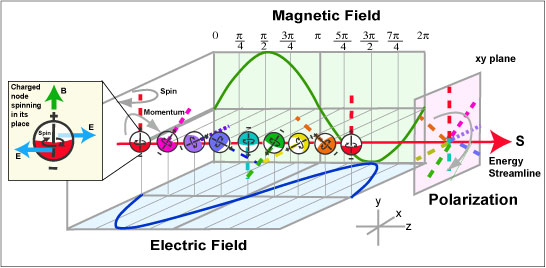
FIG. 8.  Nodes transferring their spin and forward momentum as part of an electromagnetic pulse radiating along a streamline S in the z direction. The Magnetic (B) component of the nodes’ rotation creates the electric field and Electric components (E) create the electric field. Any component of the rotation in the xy plane creates polarization.  The strength of (E) and (B), hence the intensity, is determined by the node spin. The colors are a graphic aid and have no physical significance.

1.5       VELOCITY OF INTERACTION, SPACE AND TIME

           There is no time dimension presupposed in (BU) theory, only successive ‘instantaneous’ local states of the universe. Spatial directions, i.e. dimensions, do not have an inherent reality either, but result from the geometry of the node packing. Distances exist because signals traverse different numbers of nodes in succession. However for convenience, and to keep track of the various states of a local volume of space involving many nodes, a minimum unit of time t₀ is defined using a hypothetical separation d₀ between nodes, whereby angular momentum in a vacuum free from and far away from matter, is transferred from node to node with a velocity c₀.  This is the maximum speed of light c in vacuum c= c_o = 2.99792458 times 10^8 meters per second.

(3)                    c_o = d_o / t_o

           If the nodes to which the forward momentum is transferred have a spin s₁>s₀, then the pulse will be delayed, and will travel over a smaller number of nodes, i.e. a distance, as compared to one in vacuum, where nodes have spin s_o  (FIG. 9).

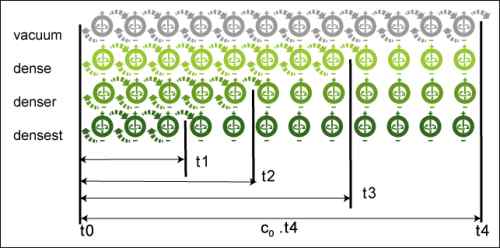
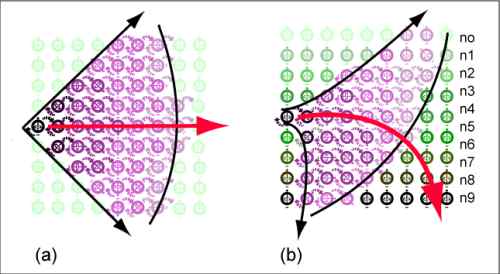
FIG. 9 radiation travels at a maximum speed of c₀ in a vacuum free of matter, but at lesser speeds where the potential is higher, i.e. the nodes are denser, spinning at a higher than the vacuum rate s_o

             Assuming that the relationship between the velocity of transfer depends linearly on the inverse of the spin of the node receiving the momentum and its orientation,  

(4)                   

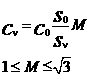
 where M is a geometrical inclination factor depending on the direction in the lattice between the donor node and the node receiving the momentum as will be explained in section 2.2 below. When the direction is orthogonal to the faces of the FCC M=1, and √3 when it is diagonal. The pulse velocity c_{v <} c_o is measured by the distance it travels compared to an adjacent pulse traveling in vacuum.  Straight-line distances are measured by the number j of nodes a signal traverses:

(5)                    d_o=j Md_o                     (j= 1,2,3…)

           A local index of refraction of space n or its inverse  can now be defined:

(6)                  

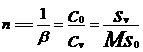
           Angular momentum spreads as energy in the lattice as light would in a transparent medium having a variable index of refraction such as the atmosphere with variable density gradients[27], or in a gradient index GRIN lens[28] as in (FIG. 10).

FIG. 10 (a) A light wave radiates in vacuum of index of refraction n_o=1 (b) In an inhomogeneous potential field of variable index of refraction the wave is distorted accordingly by refraction.  Particles (not shown) having the same momentum and traveling in the same media would be similarly ‘refracted’ (large arrows).

• Top Next

 

REFERENCES FOR THIS SECTION