BEAUTIFUL UNIVERSE

2.9       WEAK GRAVITATIONAL, BUT STRONG ELECTROSTATIC FORCES

The equations describing the gravitational force and the electrostatic force are very similar. In both cases the force between two particles is proportional to the product of their masses or charges, and inversely proportional to the product of their distance, multiplied by a constant.  However the Gravitational constant G is many orders of magnitude smaller than Coulomb's constant (k). (BU) offers an explanation for this: If the masses and charges involved are thought of as spheres, the nodes making up the gravitational field surrounding an uncharged mass will have their axes tangential to its surface. They will be normal to radial lines extended from the center of mass and the surrounding nodes in the field will experience mutual repulsion as discussed earlier. This would be true whether the nodes rotate in place or not. In the case of a charged particle (or permanent magnet) the nodes orient themselves along the radial lines so that the surface of the sphere will only have like charges (+ or -) on it. This will cause the nodes of the surrounding field to align themselves radially, strongly locked (+ with -) end to end, along the so-called lines of force making up the field. (FIG.33).

Another explanation for the low value of G known today might is that relatively massive macroscopic systems are now typically used to measure G.  A single node is immediately surrounded by just 12 other nodes in an FCC lattice. Currently a spherically homogeneous mass is assumed in deducing G from the measured gravitational forces between two spheres.  The geometrical differences between the two models should be studied to calculate, measure or deduce the true value of G on the scale of two adjacent nodes.  

Revising the value of G of would increase the value of the smallest distance assumed in nature, the Planck Length, 4.05096x10^-35 m.  which must  equal d_o the distance between nodes in the lattice. This of course does not imply that d_o equals the present value of the Planck length.

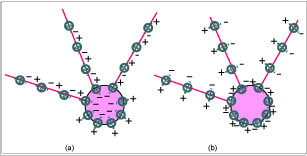FIG. 33. The weakness of the gravitational field compared to the electrostatic one. (a) A charged particle’s surface nodes are oriented normally to its surface. The adjacent nodes’ axes align themselves along the streamlines as lines of force, because of strong (+-) attraction. (b) An uncharged particle’s surface nodes are parallel to the surface and there is no strong polarity, so the field nodes’ axes are normal to the streamlines interacting weakly.

2.10    THE STANDARD MODEL

If (BU) is indeed a true model of how nature operates, various results of the Standard Model[80] would then emerge from it. Not all the results may do so, for some may prove spurious. For example the many symmetries possible in a regular FCC lattice can be compared to the concept of symmetry in the Standard Model. Symmetry-breaking would be explained because all the nodes in the (BU) universe have handedness, spinning in the same sense.  It is beyond scope of this paper to go beyond the following further suggestions:

           Particles of matter in (BU) are constructed of various polyhedral arrangements of locked nodes, as suggested in section 1.6. This concept was examined in detail by Fuller[81], and is demonstrated by Cook’s model of the nucleus³³,³⁴. In general free electrons and subatomic particles would be clusters of nodes in various polyhedral arrangements, each node either spinning in place, or  also rotating in unison with all the other nodes. This in turn suggests that the so-called force-carrying particles of the Standard Model are imaginary entities related to the geometry of the field in the volume of nodes between the surfaces of two congruent particles. (FIG. 34). The placement and orientation of the nodes on the two particles’ opposite surfaces will affect those in the volume between them.

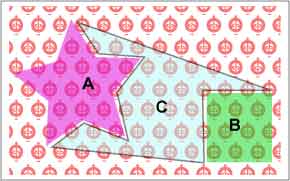FIG. 34 The concept of force-carrying particles between two particles A and B in close proximity. The states of the nodes on the surfaces of the particles facing each other and the geometry of the intermediate volume C define the interaction between A and B.  In that sense C is a force-carrying ‘particle’.

                In Internet physics chats the square root of the fine structure constant alpha was related by ‘FrediFizzx’ to the geometry of an electron surrounded a cubical arrangement of virtual particles[82], closely resembling the situations in a cubic (BU) lattice. Another researcher ‘FrankH’ relates the polarizability of matter to the Electrostatic gradient and to the gravitational force[83]. This is similar to the (BU) concept that gravity is ascribed to the twisting (i.e. polarization) of the node axes in a field surrounding matter. Finally, is antimatter made up of matter with the nodes spinning in the opposite sense, or merely structured with each 'normal' node rotated in place by (π)?  Would the two cases be equivelent?

2.11       COSMOLOGICAL QUESTIONS

As described in section 1.3 and (FIG. 1), according to (BU)   the expansion of the universe is due to local repulsion between the nodes making up space, and not to an initial explosion of a Big Bang point where and when space and time began.   Assuming that the nodes of (BU) have some sort of substance, they must have initially been compressed together into a minimum sphere (but not a point) by some surrounding force and suddenly released.  This raises the question of whether the entire (BU) exists within further dimensions that we cannot detect. In either case the electrostatic repulsion between the nodes would be the cause of a cosmic inflation ‘explosion’, and would agree with astronomical observations of an expanding universe (FIG 35).

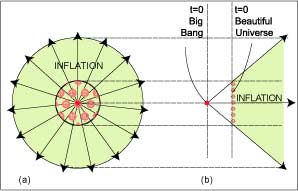FIG. 35 Big Bang theory states that spacetime started expanding from a point followed later by a period of unexplained sudden inflation. (BU) theory states that the universe started from ether nodes compacted together, but not to a point, then immediately started inflating due to mutual node repulsion. The node geometry defines space and node-to-node

This (BU) scenario implies that d_o increased from some minimum value but not zero at the time of Inflation. This in turn would affect the value of co. In other words the speed of light in vacuum was some maximum at Inflation and decreased uniformly as d_o increased, until it reached the locally measured value today.   Since the speed of light would then be slowing down all over the universe proportionate to its rate of expansion, our basic concepts of astronomical distances and time-scales must be re-examined accordingly.

As a result of linking the concept of time to that of the distance d_o in (BU), a curious conclusion can be reached:  As the universe expands, and since the nodes repulse each other, geometrical relationships between the nodes expand accordingly. Unlike in the Big Bang theory[84] where space expands with no center, the expansion of the universe in (BU) has a center. If this is true the radial distances between adjacent nodes expand less than their tangential distances. The difference is indirectly proportional to the radial distance from the center of the universe, so it is very slight. All interactions must then slow down by that amount in tangential directions.  (FIG. 36)

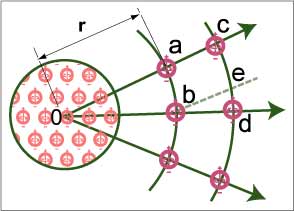FIG. 36. Does the Beautiful Universe have a center (0) and the nodes expand inhomogeneously?  If so, then the node-to-node rate of expansion along tangential ‘distances’ will be slightly larger (depending on the radial distance r )when measured tangentially than when measured radially:  While ac=bd  ,  ab<cd. This effect may only be measurable on astronomical scales.

The dark matter[85] pervading the universe and keeping galaxies from disintegrating while they rotate, will have a simple explanation in (BU): dark matter is simply the nodes of the vacuum which surrounds all matter from atoms to galaxies. Their combined and uniform repulsion would be experienced as a pressure directed at the surface of all matter (FIG. 37). This same repulsion explains the 'Dark Energy' [94] now conjured up to explain the discovery that the expansion of the universe is accelarating.

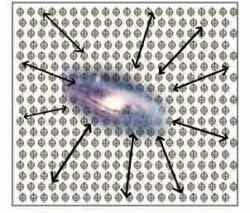FIG. 37 ‘Dark Matter’ and 'Dark Energy' are different outcomes of the same phenomena: the mutual repulsion of charged spinning ether nodes of the lattice. This repulsion acts as a 'force' on matter it surrounds. It also accounts for of the accelaration of the expansion of the Universe.

The Bekenstein-Hawking result that the entropy of a black hole is directly proportional to the area of its event horizon[93] somehow resembles the (BU) notion that mass can be equated to the momentum contained in a surrounding spherical shell, as in Fig. 11 and the discussion in Sec. 1.6.

3.     EXPERIMENTAL TESTS OF (BU)

Various aspects of the theory may be testable. Some possible approaches are:

3.1     THE EVIDENCE OF DIFFRACTION AND DE-DIFFRACTION

The fundamental reason radiation fields diffract is easily explained in the (BU) model: nodes transfer energy to many nodes around them, so that the wavefront behaves as if it is made up of Huygens wavelets[86] centered on each node. According to Tamari’s Streamline Diffraction Theory[87] and based on the wave equation for continuous fields (i.e. not as in the discrete space of (BU)), the diffraction of a radiation field could be prevented, i.e. de-diffracted (DD). If the initial conditions mimic those of a time-reversed diffracted wave, a (DD) wave will be produced.  DD may occur only if the vacuum had no role to play in the diffraction process, otherwise the granularity of space will prevent it.  An experimental failure of DD can be taken as a proof of (BU) theory, as detailed in (FIG. 38). So far, the only experimental result using light indicated a failure of DD[88], but more refined experiments will be needed to reach a definite conclusion (FIG. 38).  Similarly, simulations have shown that time-reversal of a quantum system is possible[89]. If this is confirmed experimentally it would falsify (BU) node-to-node interactions as assumed in this paper.

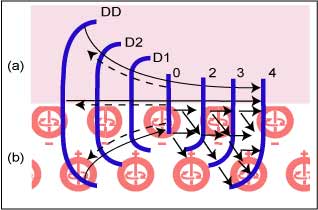
FIG. 38   Diffraction  of waves in vacuum is shown in the left half of the in the figure in cases of continuous classical fields (a) or in a volume of  discrete (BU) nodes (b):  Wave (0) leaves an aperture travels to the left, diffracting into wavefronts  D1, D2, DD… De-diffraction theory states that the reversed wave, (DD traveling to the right) will continue without diffracting as the upper portions of waves 0, 1, 2… In the (BU) field (b), wavefront (DD) will diffract again after (0), because the momentum is spread out from each node in wavelets from each node (small arrows).

3.2       A VACUUM DIFFRACTION GRATING AND EVIDENCE OF A DODECAHEDRAL              COSMOLOGICAL STRUCTURE?

An electromagnetic beam formed within an optical cavity in vacuum will have its nodes energized in a fixed pattern of maxima and minima. This can be used as an immaterial diffraction grating to scatter another wave crossing the optical axis of the first beam normally (FIG. 39).

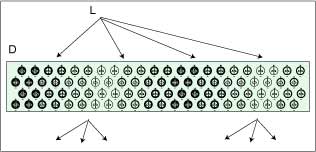FIG.  39. Light shined from L through a region of vacuum containing a standing optical wave D.  The standing wave will act as a diffraction grating, demonstrating the reality of the nodes.

    Similarly, the vacuum lattice structure might be the explanation for the recent observation that the microwave background temperature distribution suggests a dodecahedral ‘shape’ for the universe. [90]It is more probable that the micro structure of the FCC lattice geometry of the nodes, within which a dodecahedron can be outlined, is the physical cause for this result.

3.3         TIME-RESOLVED HEAVISIDE CONTRACTION?

In Section 2.4 and (FIG. 26) it was shown how a force impinging on stationary matter will compress each atom into an ellipsoid, shortening the overall length accomplishing the Heaviside contraction (Eq. 16) before the object actually starts to move at the velocity v.  If a force is applied a very short time on the short end of a very long dense rod, it will be possible to actually measure this contraction before the rod starts to move.

 3.4        GRAVITATIONAL / ELECTROSTATIC FIELD ANOMALY ON A SPHERE?

[91] which implies that any continuous vector field tangent on a sphere must have a point where the vector is zero.  In other words combing a hairy ball always leaves a point uncombed. The gravitational, field surrounding a spherical particle will have a vortex on the surface where the gravitational and electrostatic fields will be null.  Buckminsterfullerene³¹, ³² C₆₀ molecules may be ideal candidates to test this idea with, since they are spherical and are small enough that a gravitational anomaly would be prominent (FIG. 40).

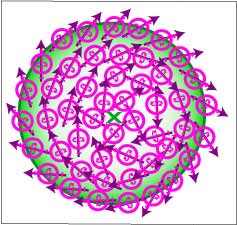FIG. 40.  Brouwer’s theorem in topology states that a field of vectors on the surface of a sphere always has one vortex.  The gravitational field of a particle will have a spot where its gravity is zero. Nodes oriented with their axes tangential to a sphere’s surface will include a group whose axes rotate 360◦ relative to each other canceling any forces there (X). This in turn will create a null field along a cone whose axis is extended from the center of the sphere through X and into space.

3.5       COSMIC TIME DILATION AND VARIATIONS IN SPEED OF LIGHT?

As explained in section 2.11 and (FIG.36),  if the (BU) expansion started from an explosive inflation with a center, then the speed of light, and hence the measurement of time, will be faster measured radially than tangentially. The effect is proportional to the radial distance from the center. Is this effect detectable in astronomical measurements?

            More critically, the measured speed of light c_m may also depend on the node-to-node distances of the local lattice. As described in Section 2.7, and seen in (FIG. 29a.) this distance can vary by a factor of F_L for a square lattice depending on the direction angle of propagation within the lattice.

(22)                                          c_o=c_mF_L

This also depends on which lattice packing actually exists in nature.  Experiments can be devised similar to Michelson and Morley’s but with the interferometer arms at various angles not just ninety degrees to each other.

4.         CONCLUSION

A new physically realistic universal ‘building block’, a spherically symmetrical charged node, has been proposed to re-construct physics with, and various known phenomena were examined from the few simple rules of how it behaves. The model explains some of the known results of Special and General Relativity, Quantum Mechanics and the Standard Model, but without their assumptions, such as a point photon, flexible spacetime, the constancy of the speed of light, or the reality of   probability functions.  A universal self-assembled regular lattice of nodes creates space; and their comparative rate of transfer of angular momentum to adjacent nodes is used to describe time. While the nodes themselves do not move within the lattice, radiation is a spreading ‘falling domino’ pattern of such momentum transfer between the nodes. Motion of matter is a self-convolution of a pattern of nodes locked by mutual coulomb forces in a (+-) tensegrity structure created by the balanced attractive and repulsive forces between adjacent magnetic nodes.  Node spin regulates signal transfer velocity, therefore node energy can be regarded as proportional to a local index refraction of the universal medium. The Hamiltonian Analogy is then used to describe energy transport across the lattice.  Various aspects of 20^th Century physics and cosmology are explained from the Beautiful Universe (BU) model and various experimental tests of the theory are proposed. The treatment is elementary and qualitative, and suggestions for improving the model, proving or disproving it are welcome.

5.         ACKNOWLEDGEMENTS

Online research for this paper made it possible to read the ideas of scores of  physicists dissatisfied with the state of physics today. There was much that I could not understand or that I did not agree with, but the current ferment was always stimulating. Thanks are due to the online physics community aiming to reconstruct physics on a new basis. Some papers needed more study but I lost their reference, such as a highly mathematical paper by a Korean physicist who described a unified theory based on dipoles.  I thank Gabriel LaFreniere[57] for interesting correspondence and for his beautiful and instructive simulations of Lorentz contractions and Doppler shifts in matter waves.  Norman Cook[33] kindly sent me the amazing NVS software he developed for simulating nuclear structures, a concept that compliments my ideas for physics in a regular universal lattice. I thank him for his encouragement and for proofreading the text.  Rev. Dr. John Polkinghorne [92] warned me that an attempt to combine quantum theory and gravity is “extremely difficult and has resisted the efforts of very great experts”. I did not heed this wise and kind advice, and foolishly but happily spent many years of difficult research, often in areas way beyond my capacity, as can be readily seen in this paper. Dr. Dennis de Lang’s computer assistance was invaluable in the preparation of this paper. His studious example and encouragement, and those of Dr. Kaveri Rangappa and Dr. Bonnie Schupp are warmly acknowledged. I thank David Shapiro for his positive response after reading an early version of the introduction to this paper. Most importantly this work would not have been possible without the loving support of my wife Kyoko and our daughters Mariam and Mona

________________________

• Previous Top

REFERENCES FOR THIS SECTION

© 2007-2008 VladimirTamari