BEAUTIFUL UNIVERSE

1.6       MATTER

           While radiation is a dynamic spreading group pattern of momentum passed from node to node, matter at rest is a pattern of nodes with their axes locked in position or rotating in place, the result of mutual attraction and repulsion in static or dynamic equilibrium within the lattice.

           The axes of locked nodes are oriented along a direction defined by two angles according to some chosen coordinate system. The nodes form edges or vertices of 3-dimensional polyhedral structures, the simplest of which is a tetrahedron. For example the two nodes of FIG. 3 have their axes aligned along the same line. Here the   twist in the node polarity defines the quantum spin (qs) of the particle. (qs) describes geometrical orientations and symmetries, and not spin (s) in the sense of rotation used above.  The 3D geometry allows larger pieces of matter, existing within larger polyhedra, to have many more possible orientations. A node cannot change its axis without affecting those of the surrounding nodes with the locked nodes both within matter and in the surrounding field up to infinity. To do so requires a lot of energy, as illustrated  in the hypothetical case of a unit particle made up of two adjacent nodes locked as a particle as in (FIG. 11).

           A hypothetical ‘explosion’ of two-node matter in a vacuum lattice is imagined. At time t= t₀ all nodes except node A are assumed to be oriented in the same upwards direction and having unit spin (s). Due to some influx of momentum from the left, (not shown) A untwists, its axis of orientation and rotates by 180° (π radians) suddenly, while its twin remains fixed. This twist constitutes forward momentum, but its direction is not radially outwards in the plane of the spin axis, but normal to that axis. The adjoining nodes adjust their orientation accordingly, and the twist-induced momentum is transferred as a pulse radiating as a hemispherical shell at a velocity c_o .The number of nodes J on any hemisphere of radius (r) is J=a_n2 π r² where (a_n) is the average number of nodes per unit area of a large sphere.  In one second the shell reaches the nodes aligned on hemisphere H of radius c₀ (the distance energy travels in vacuum in one second) so that J_c0= a_n 2π c₀². In this one second each of the J nodes has twisted by π or less, according to its position on H the total change. A full twist in one second represents a gain of angular momentum of (h).

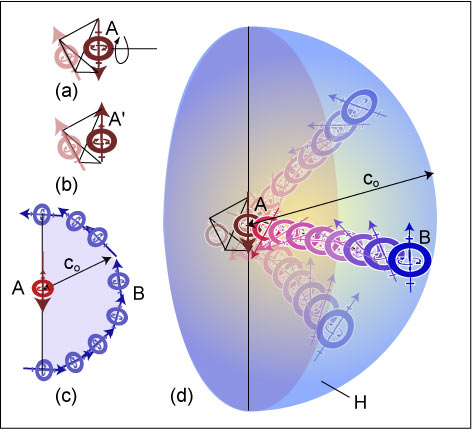
FIG. 11 A hypothetical example of matter releasing its locked energy. (a) Node A in vacuum is locked with another node to form a particle. (b) Forces (not shown here) force Node A to rotate by π about an axis normal to its spin axis, acquiring state A’. (c) The released momentum from A causes a twisting effect to be transferred radially from node to adjacent nodes, and after one second the effect reaches nodes such as B, aligned in a hemisphere H of radius c_o (d)  Lattice nodes on the surface of the hemisphere of surface area 2πc_o² now contain all the momentum originally found in node A in its locked state.  A reversed version of this process is also possible, whereas the nodes on the surface transfer their momentum inwards creating matter by twisting A’ into locked matter A.

           Assuming that an average node twists by angle b, where 0<b<p, and since there is a vast number of nodes on H, any fractional (h) in the total can be disregarded, the total momentum M acquired by the nodes on H is:

(7)                    M_H=2π a_n bhc₀²  

           Equating M_H with the rest energy E originally locked within A, and letting

(8)                    m= 2 π a_n bh

(9)                    E = m co²

           (Eqs. 8 and 9) define an attribute (m) of matter in units of angular momentum (h).  

           The process imagined above is reversible, and can be used to describe the creation of matter from the implosion of spin from nodes H. The angular momentum reaching the center from all directions simultaneously causes A’ to become twisted into its ‘matter orientation’ A.  In a realistic situation, the particle of matter will have its own infinite gravitational field, where each node’s axis will be twisted to some extent, adjusting to the orientation of the adjacent nodes. Also the spin of the originating nodes may be much more than unity in the case of massive particles.  At large distances from a particle the field will tend to be more spherical but very close to asymmetrical particles the surrounding field will also be inhomogeneous.

           The resulting equilibrium of locked nodes of matter particles is very similar to that of the Tensegrity sculptures of Kenneth Snelson[29] and Buckminster Fuller. Rods under compression are freely suspended in space without touching one other, held by wires under tension joining the ends of the rods (FIG. 12).

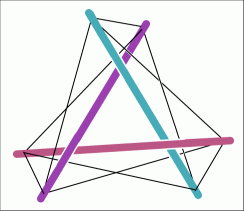FIG. 12. A basic floating compression (tensegrity) structure, by Kenneth Snelson, the inventor of the concept. The rods under compression are held in place without touching each other, by taut strings.  In (BU) theory the nodes making up particles of matter are similarly held in place without physical contact, because the balance of attractive and repulsive Coulomb forces between the nodes. The rods resemble a basic weave or knot pattern.

 (Adapted from http://www.kennethsnelson.net/icons/struc.htm )

           Such sculptures need one or more anchor point in the ground to stay in equilibrium, but in the (BU) lattice the locked nodes are surrounded by the repulsive forces of the surrounding gravitational field.  Svenson himself realized the importance of this sort of constructivist principle to build a model of the atom.  He discovered another principle relevant to the architecture of the nucleus: a system of magnetized tops arrayed symmetrically in a spherical formation would induce each other into synchronous rotation (FIG 13).

FIG. 13. Kenneth Snelson’s illustration of the magnetic tops whose axes meet at the center, to model nuclei. The number of synchronously rotating tops making up each model are (left to right): 32, 18, 14, 10, 8, 5, 2.

From http://www.kennethsnelson.net/icons/atom.htm )[29]

           Buckminster Fuller (who coined the word Tensegrity) believed that all nature is a ‘synergy’ of structure and energy based on the tetrahedron[30]. He speculated about nuclear structure in terms of nested polyhedra (FIG. 14) based tetrahedral design principle. The spherical domes he invented are based on this design philosophy. Nature seemed to agree with this when the molecule C₆₀ called the Buckminsterfullerene[31],[32]  was synthesized and found to follow the same design principle as the domes (FIG. 15).

FIG. 14 A drawing made in 1948 by R. Buckminster Fuller, analyzing the space-packing possibilities of structures based on the tetrahedron. From Synergetics by R. Buckminster Fuller[81]	FIG 15 Schematic diagram of a Buckminsterfullerene C 60 molecule. From http://sbchem.sunysb.edu/msl/fullerene.html

           Using an alternative formulation of (QM), Cook[33], [34] has demonstrated how nuclei can be modeled as various particles in a Face-Centered-Cubic lattice forming a crystal-like structure (FIG.16).

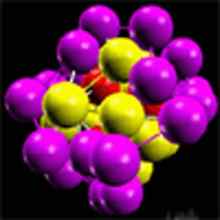
FIG. 16. Norman Cook’s model of nuclear particles from his Nuclear Visualization Software shows a distinctive crystal-like arrangement in a face-centered-cubic FCC lattice.

From http://www.res.kutc.kansai-u.ac.jp/~cook/NVSIndex.html

           Stedjee examines the possibility of using the neutrino, the smallest known particle as a building block for all matter[35]. A common feature of all the above proposals for matter is that they rely on a principle of constructing polyhedra from simple building blocks. In (BU) only one type of ‘block’, the node, will be required. 

1.7         GRAVITATION

            If the process of adding angular momentum from the outer shells of (FIG. 10) continues after the nucleus of matter is formed, all the nodes surrounding the pyramid will acquire more spin, aligning themselves radially to the orientation of the locked nodes at the center.  This surrounding pattern of spinning nodes is also locked in place, with the angles 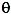 between congruent nodes decreasing with distance from the center, the results of self-assembly of the nodes adjusting their orientation to reach a state of minimum energy.

            Matter and the infinite field of surrounding nodes now achieve a state of equilibrium: matter within its gravitational field (FIG.17) can be thought of somewhat as the internal pressure inside a bubble of gas balancing that of the surrounding fluid.

FIG. 17.  Two nodes forming the simplest of particles are oriented along opposite sides of the tetrahedron in the center of the figure. As shown by the arrows they induce the surrounding nodes to orient their axis accordingly to form the surrounding gravitational field. The nodes are shaded to indicate their weakening spin energy as their distance from the center increases.

           The nodes do not necessarily stop rotating when locked in place, but can create a standing gravitational wave pattern with a wavelength inversely proportional to the mass, recalling the de Broglie hypothesis. Is this is the result of mutual interference or of resonance within matter?  If matter as a whole rotates or decays a gravitational wave is radiated accordingly.

           Starting from the spinning nodes at the surface of matter, each node’s angular momentum balances that of two or more further out in the network, so that nodes on a spherical surface centered on matter will be equipotential. To ensure the field’s equilibrium, nodes on any spherical shell of a radius r surrounded matter must have a total energy equal to that of nodes on any other shell. It becomes clear that the gravitational potential - i.e. the total spin of a given node- (_grav) is both dependent on the original mass’ total energy and inversely proportional to the surface area of the sphere of radius r it lies on.

(10)                  _grav= G₀ (∑ angular momentum of all the nodes locked in matter) / r²

           Which is Newton’s famous result[36] interpreted in terms of (BU) where the summation is the mass of the particle, and G₀ is the experimentally derived gravitational constant, relating node spin and momentum with the amount of twisting of adjacent nodes. In (BU) G₀ is related to the repulsive force from node to node (which may be less than the experimentally derived G used for macroscopic objects as will be discussed below.

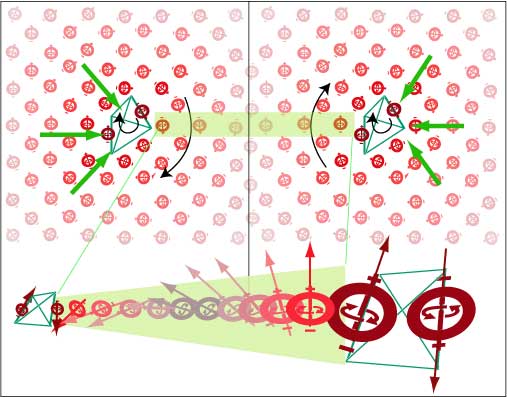
FIG. 18 Gravitational attraction is due to the fact that all the nodes making up the particles and their surrounding gravitational fields all spin in the same sense (shown by the curved arrows inside the nodes) . This aligns the field nodes according to polarity (large curved arrows).  At the center of the ether volume between the particles (shaded area, shown in detail at bottom), the nodes experience (+ -) attraction instead of the (++) and (- -) repulsion. This initiates chirality i.e. a spiral twist in the central nodes and the effect is carried on back to the nodes. The relative momentum in the nodes surrounding the particles on their opposite sides now becomes stronger than that of the nodes in facing sides. This imbalance in momentum ‘pressure’ constitutes a force (large arrows) which starts the gravitational acceleration of the two particles towards each other.

           If two clusters of matter A and B exist at some distance from each other, the nodes along lines joining A and B will have the nodes in their fields oriented in opposite directions. This is because all nodes in (BU) spin in the same direction (clockwise or anticlockwise relative to their own magnetic poles).  In a situation such as that of (FIG. 18), the field nodes along a line AB experience disequilibrium. Their spin axes angles  change, relieving the induced forces on them, and uncoiling like a spring. This decreases the momentum of the nodes along AB. To restore balance, angular momentum is transferred to A and B from the outer surrounding nodes, which forces them to move towards each other filling the energy void created along the line AB.  The process of uncoiling the nodes along AB continues, until the system finally finds equilibrium when A and B collide into each other.  More complicated situations involving three or more objects involve similar processes.

1.8       DYNAMICS:  FORCE, INERTIAL MASS, AND MOTION

           In (BU) a particle of matter is a pattern of nodes locked in place in different orientations. When an influx of new angular momentum arrives from a given direction the added energy is absorbed by the particle, ‘forcing’ the nodes of the particle to spin faster. This force initiates a complex process of transferring the extra momentum of all the nodes of matter in the same direction as the original ‘force’. Matter experiences motion (FIG. 19).

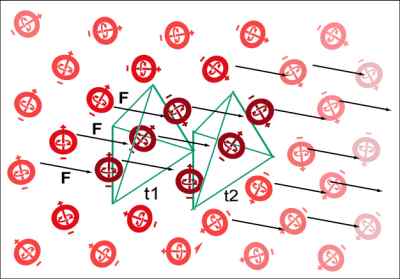FIG. 19 Motion of a particle across a lattice of nodes: the nodes themselves do not move, only their pattern of spin. At time t1 the particle at left experiences new momentum impinging on it as a force (F) The particle’s spin pattern is translated to its new position at time t2. The surrounding gravitational field nodes’ pattern (right) experiences a similar transfer in position.

           It is essential to examine the minute changes that would then occur to the geometry of the particle as it changes states.  In both optics and data processing, when an image or signal is made to cross over itself linearly without losing its shape, the process is called a self-convolution.  When a particle experiences a force, the momentum added to the first nodes in its path at the particle’s edge absorbs this momentum, which affects both its energy and orientation. This in turn affects the adjacent nodes.  Self-convolution involves all the nodes in contact with the force, and continues within the volume of the particle, until all the impinging new momentum is absorbed (FIG. 20).  

           The process is not confined to the nodes within the particle itself. The added momentum is then directed from the particle to its own surrounding gravitational field.  Unlike the case of an electromagnetic wave traveling in vacuum at the maximum speed of light c₀, the particle’s pattern is now translated to the gravitational field at a rate   v < c₀ . The reason for this slower speed is that the index of refraction of space within the particle and in its gravitational field is n>>1. The particle’s forward momentum is being dragged by of its own internal energy and that of its surrounding gravitational field. That is why matter has inertial mass, a property that only manifests itself when an external force is applied.

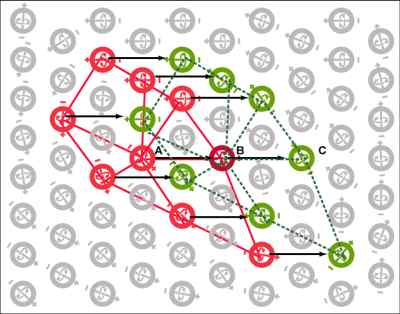FIG. 20. Motion of a particle involves a process of self-convolution of its constituent nodes.  The arrows link the nodes of the particle in its initial state and the nodes after it moves to the right (dashed lines). Similar transfer of states (not shown for clarity) occurs in all the surrounding nodes.  In this simple example, each node’s state is transferred to a ‘new’ node. The state of node A however is added to that of B, and B’s to C. More complex particles involve many more such overlapping states.

           In the case of gravitational attraction the two particles moving towards each other also experiences self-convolution. In this case however, there is no gravitational ‘force’ as such causing the motion, only an imbalance of the repulsive forces of the nodes surrounding both particles.

           To summarize this process:  matter absorbs new forward momentum as a force applied in one direction. Its nodes absorb this force and transfer the energy internally from node to node, affecting both the rate of spin and the orientation of the absorbing nodes. Self-convolution proceeds over across the object and continues over its pre-existing gravitational field. In its various states the particle shifts as a whole pattern of nodes by steps d₀ and at a certain velocity v depending on the original energy or mass of the particle’s nodes, and the force.

           Another way to visualize convoluted motion is through the concept of Fresnel drag[37] [38], when the velocity of light c_fluid in a fluid of index of refraction n moving at a velocity v, becomes:

(11 )                  

(13)                    

Where(_fresnel involves the same variables as

(14)     

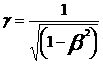
           This is the relativistic term familiar in the equations of (SR) and (GR), affecting time, mass and length of a moving object.  In (BU) the moving particle is conceived of as a fluid pattern of nodes transferring energy at a velocity (v). The pattern of matter moves as a group with velocity v, but the momentum inside the pattern moves at a faster velocity v_fresnel . Such an effect can also be observed in ripples in a pond when the circular outline of a group of ripples is spreading at a certain speed, but the ripples appearing from the inner rim move at a faster speed and disappear at the outer rim. The same phenomena has been analyzed by LaFreniere in terms of a Doppler shift[39] in the frequency of the signal in the moving particle.

 Since there is no time dimension in (BU) all these changes will be merely successive changes of the state of the nodes as a whole. Motion as such is perceived only when an observer remembers and compares the various states, or a record is kept such as frames in a movie film, or as a record in computer memory is made.

1.9       SUMMARY OF THE (BU) ASSUMPTIONS

           The basic physical structure of the Beautiful Universe  model outlined above is extremely simple, describing a universe made up of identical charged particles (nodes), self-assembled into a locally regular network. These nodes never change their positions in the lattice, but interact only with adjacent nodes by transmitting the angular momentum they carry. This occurs without loss, through effects similar to electrostatic attraction and repulsion. All interactions are linear, and follow the logic of cause and effect.  The state of each node is defined solely by the rate of spin and the direction of its angular momentum. Any change in the state of any one node is transmitted through contiguous nodes sequentially to all the nodes in the universe at a local velocity v=c_o/n, where n =>1 is a node density index, comparing its actual spin energy to that of a node in an ideal vacuum. In this case an ideal vacuum is one not only free from radiation and particles, but is not part of any gravitational field of matter, however far. Patterns of nodes can assemble into dynamic radiation fields in space, or lock themselves as matter including its infinite surrounding gravitational field.  A local volume of nodes is in equilibrium when each node’s forward momentum equals that of the vector sum of the adjacent nodes. Otherwise, when a transfer of momentum, radiation is created, or matter patterns are created, made to move or to rotate.  Disequilibrium also initiates the emission or absorption of radiation by matter, and in extreme cases the unlocking of matter into radiation. In (BU) the maximum signal velocity between nodes is c_o the velocity of light in an ideal vacuum.

• Previous Top Next

REFERENCES FOR THIS SECTION